Do you plan a trip to the field? Need to be able to range targets, but don’t want to carry specialized rangefinding equipment? Such questions get asked often around the internet, but most people say it can’t be done without a mil-dot or rangefinding scope reticle and a set of mathematical formulas – often requiring a calculator, if you want reasonable precision – to compute distances. I’m writing to tell you that there is a much simpler way, faster and with little or no math, which is just about as effective, and requires only one very common shooter’s tool that you probably already own and carry on every trip to the field.
All you need is a second focal plane (or SFP, it means that the reticle stays a constant size relative to your eye, rather than growing or shrinking with magnification power) variable power scope with some type of reticle marks (a standard duplex will serve) and an accurately-marked magnification adjustment ring. This method involves using the magnification ring like a simple slide-rule – those mechanical cheat sheets that scientists once used to get serviceable figures without engaging in intensive math, before general availability of scientific calculators rendered them obsolete.
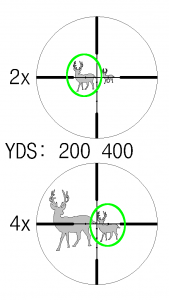
Two deer, left is at 200 yards, right is at 400. Top, viewed at 2x magnification, bottom, viewed at 4x.
So how do you do it? Lets say you know that a deer’s average length is two ticks wide on your reticle when viewed at 1x at 100 yards away. In the field, you spot the deer at an unknown distance. Zoom in until two dots on your reticle match the length of the deer. Now look at your magnification ring and estimate the magnification factor. If you zoomed in to 4x, the deer is 400 yards away. If you zoomed in to 6.5x, the deer is 650 yards away.
To understand how this works, you need to take a moment to visualize the way distance perception works.
If an object is 100 yards away, a given object will appear a given size. At 200 yards away, it will appear one half (1/2) the size that it appeared at 100. At 700 yards, an object will appear one seventh (1/7) the size. Likewise, when using a zoomable scope, 2x magnification will make an object appear twice its size. 7x will mean it appears 7 times as large. Notice a connection?
Put these two mechanics together and you will happen upon a useful phenomenon – if an object is 100 yards away, and you view it at 1x, it will appear a certain size in relation to your reticle markings. If you move the target to 300 yards away, it will appear 1/3rd the size; however, if you then zoom in to 3x, the object will again appear to be the same size as a 100yd object at 1x. Thus, by using your reticle as a ruler and adjusting magnification to match, you can estimate ranges without doing any math.
This will also work if you have a scope that doesn’t go down to 1x. Say you have a 3-9 scope. All you have to do is know how your target will measure against your reticle with 3x magnification at 300 yards. This also works with meters, or any other measurement unit, as long as you use the same unit for all measurements.
What if your magnification ring only goes up to, say, 4x, and your target is farther than 400 yards away? Simply adjust your magnification so that the target appears half the size it would be at 1x at 100 yards, then multiply the magnification by two. For example, say you know a deer should measure the length of two dots on your reticle. Adjust the magnification so that the deer spans one dot. Check your magnification – if you were at 3.5x, the deer is 700 yards away. The same technique will work with placing a target at thirds or fourths against the reticle – just multiply the magnification by 3 or 4, accordingly.
Conversely, what if your magnification ring only goes down to 5x, and your target is closer than 500 yards away? The opposite technique will work. Measure the target at 2, 3, or 4 times the size it should be against your reticle, then divide your magnification by that amount. So if you see your deer closer than 500 yards, you might align it to 8 dots on your reticle, which is four times the size. If your magnification is at 6x, divide by four and you’ll know the target is 150 yards away.
At the time of the original writing of this article, I haven’t seen this particular method posted anywhere else on the web. I’ve seen similar ones that involve manually marking the magnification ring with the distances at which a target’s size correlates with the reticle, but I have not seen one like mine that correlates the magnification and distance, directly. I believe that my method can be easier to work with and more versatile if you are familiar with the measurements of your reticle when [x mag]=[x00 yards].
Thanks for reading, hope you found this information useful.